本周把LeetCode探索-初级算法的其他部分做完了,主要有两道排序、两道动态规划、两道设计, 还有数学和其他类别的题目。这些属于简单级别的题目,算不上难,想一会儿还是能做出来的。 这里把一些比较让人惊叹的解法记录一下。
88.合并两个有序数组
给定两个有序整数数组 nums1 和 nums2,将 nums2 合并到 nums1 中,使得 nums1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n。
你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素。
示例:
输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
输出: [1,2,2,3,5,6]
个人解法-88
这个题目限定用 nums1 来保存合并后的结果,要求in-place,所以不能直接用合并排序。可以先将 nums2 添加到 nums1 后面,再对 nums1 进行原地排序。
由于给定的两个数组都是有序的,可以用插入排序来完成。
代码如下:
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
for i in nums2:
j = m - 1
# 由于 nums1 是有序的,只需要将待插入的元素 i 与 nums1 最后一个元素比较
# 如果 比 nums1[j] 小, 则 nums1 中比 i 大的元素都向后移一位,给插入 i 提供空间
while j >= 0 and nums1[j] > i:
nums1[j+1] = nums1[j]
j -= 1
nums1[j+1] = i
双指针解法-88
用插入排序提交通过后,看题解有一个双指针法比较有意思。
这个方法的思路利用这两个都是有序的条件,分别在两个数给中维护两个从后开始的指针 p1 和 p2 ,
两个指针分别对应两个数组中最大的元素,如果 p1 < p2 , 那么 p2 就是两个数组中最大的元素,
理应排在 nums1[m+n-1] 的位置, 然后 p2 指针向前一位,继续比较,直到 p1 或 p2 有小于0时结束。
图示:
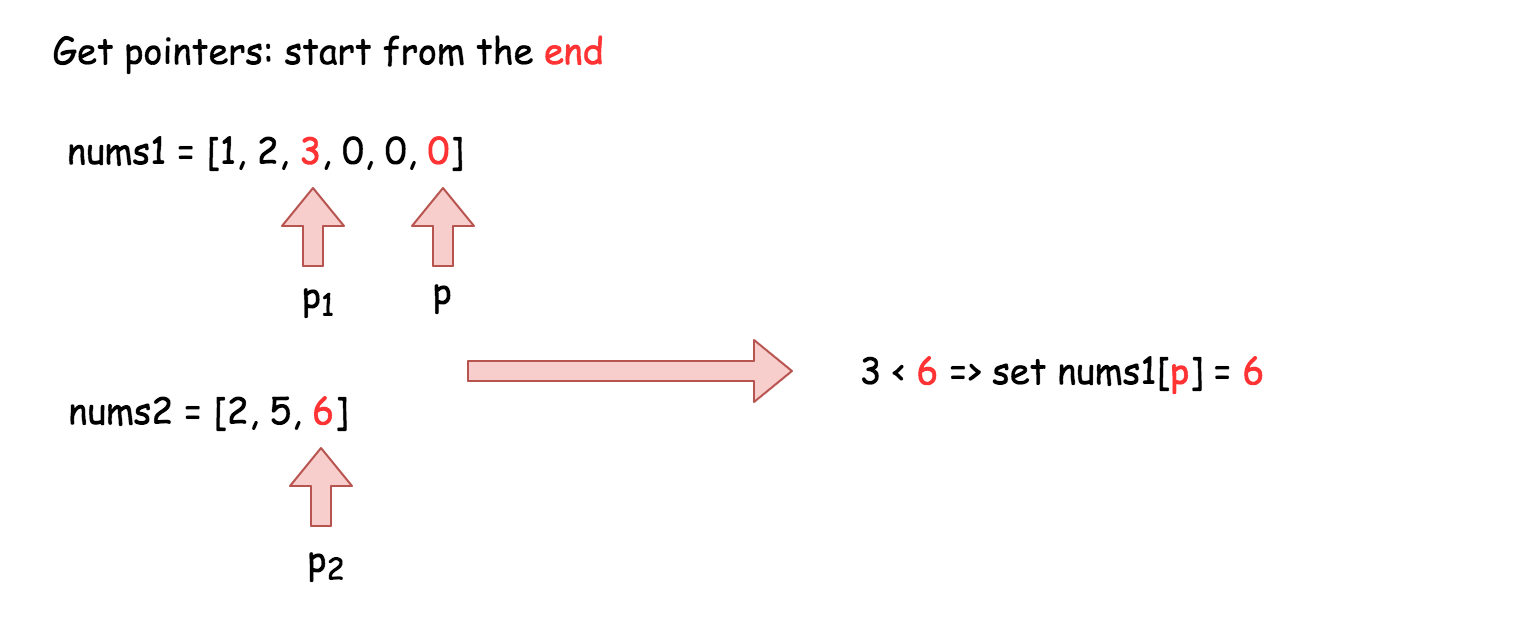

代码如下:
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
p1, p2 = m-1, n-1
p = m+n -1
while p1 >= 0 and p2 >= 0:
if nums1[p1] <= nums2[p2]:
nums1[p] = nums2[p2]
p2 -= 1
else:
nums1[p] = nums1[p1]
p1 -= 1
p -= 1
# 当循环结束时,有两种情况,第一种是 p2 = -1 此时 nums2 全部合并到 nums1 中
# 当 p >= 0 时,代表还有 nums2 中的元素未合并到 nums1 中,需要合并进来
nums1[:p2+1] = nums2[:p2+1] # 这句代码很精妙,只有 p2 >= 0 时才生效
204.计数质数
统计所有小于非负整数 n 的质数的数量。
示例:
输入: 10
输出: 4
解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
个人解法-204
质数的问题之前在SICP中遇到过,所以并不怕。判断一个数字 N 是不是质数,只需要看它能否整除小于 sqrt(N) 的质数。比如这个数是101,101开方后向上取整为11,所以我们只需要看101 能否被小于11 的质数整除,即用 2、3、5、7 四个数去尝试就够了。具体的数学解释是,因子有对称性,我们只用遍历小于到 sqrt(N) ,不明白的话,可以自己多在纸上比划比划。
将这个变成代码,需要维护一个素数的列表。
class Solution:
def countPrimes(self, n: int) -> int:
def isPrime(n, primes_list)
for i in primes_list:
if i * i > n:
break
if n % i == 0 :
return False
return True
# 由于 2 和 3 不符合上面的约定,我们单独论
if n <= 2:
return 0
if n == 3:
return 1
primes_count, primes_list = 2, [2,3]
# 这里我们稍微优化一下,在循环时把偶数去掉
for i in range(5, n, 2):
if isPrime(i, primes_list):
primes_list.append(i)
primes_count += 1
return primes_count
这个算法个人觉得还可以,但是提交没有通过,最后一个测试用例 n = 1500000 时超时了。
埃拉托斯特尼筛法-204
这个方法是高效的素数筛法,思路如下:
- 从2开始,所有2的倍数都不是素数,划掉。
- 然后是3,所有3的倍数也不是素数,划掉。
- 接下来是5,(4已经划掉了) 5的倍数划掉。
- 接下来是7,(6也被划掉了) 7的倍数划掉。
至此 120 以内的所有非素数都已经被划掉了。只剩下数一数120范围内剩下没有划掉的数,就是素数的个数。
这个算法的动图演示如下:
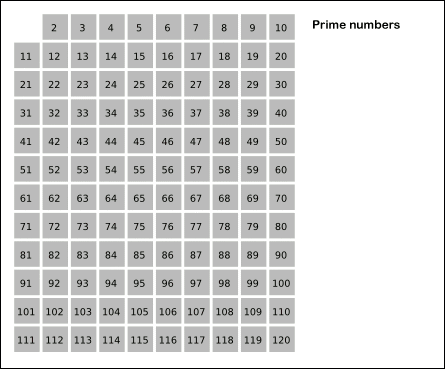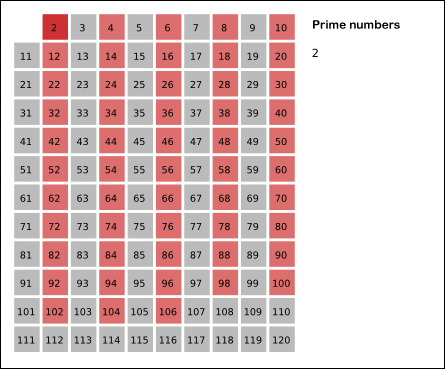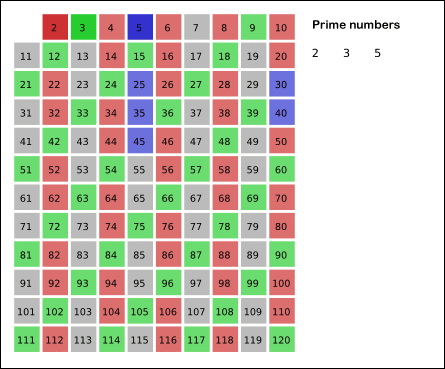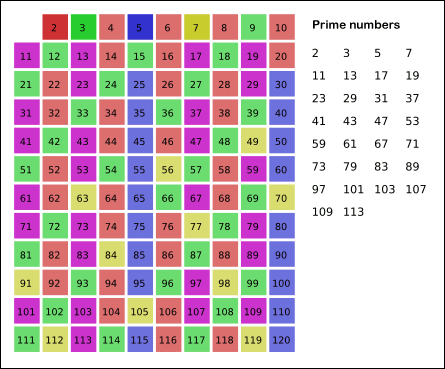
代码实现:
class Solution:
def countPrimes(self, n: int) -> int:
if n < 3:
return 0
prime_bool = [1] * n
prime_bool[0], prime_bool[1] = 0, 0
i = 2
while i * i < n:
if prime_bool[i]:
prime_bool[i*i:n:i] = [0] * len(prime_bool[i*i:n:i])
i += 1
return sum(prime_bool)
这个算法很牛叉。中间 prime_bool[i*i:n:i] 这个语句也很精妙,选中i的倍数,属于Python 特有的语法糖了。我用这个代码跑到160ms,100万级别的数也轻松通过。
当然,还有20ms的牛叉解法,就是把最大的四个测试用例直接返回,简直是鬼才。
326.3的幂
给定一个整数,写一个函数来判断它是否是 3 的幂次方。
进阶:
你能不使用循环或者递归来完成本题吗?
示例 1:
输入: 27
输出: true
示例 2:
输入: 0
输出: false
示例 3:
输入: 9
输出: true
示例 4:
输入: 45
输出: false
题解-326
这道题比较简单,下面列三个解法
普通青年解法:
class Solution:
def isPowerOfThree(self, n: int) -> bool:
while n >= 3:
if n % 3 == 0:
n /= 3
else:
break
return n == 1
3的幂嘛,如果能除3,就是一直除3就好了。
文艺青年解法:
class Solution:
def isPowerOfThree(self, n: int) -> bool:
temp = 1
while temp < n:
temp *= 3
return temp == n
我一直乘也可以啊,乘法可是比除法好做。
神仙解法:
不使用递归和迭代
class Solution:
def isPowerOfThree(self, n: int) -> bool:
return return n > 0 and 1162261467 % n == 0
因为给定范围是整数,那么整数范围2**31内最大的3的幂是3**19,那直接用这个数来试一下能否整除 n 就可以啦。
118.杨辉三角
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
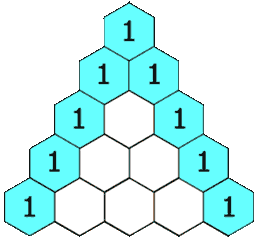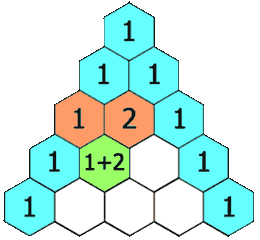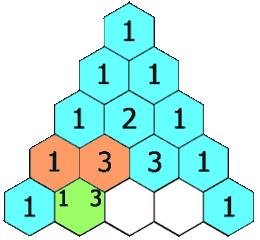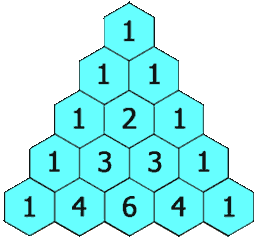
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
个人解法-118
杨辉三角,也叫帕斯卡三角形。这个题我想了半天,最后用动态规划求解。
先按给定的n生成一个全为1的三角形,再按每个数是其左上和右上的数之和来重新赋值。
代码如下:
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
res = [[1]*(_+1) for _ in range(numRows)]
for i in range(2, numRows):
for j in range(1, i):
res[i][j] = res[i-1][j-1] + res[i-1][j]
return res
这个方法不错,比较好理解。
取巧解法-118
通过观察,可发现当前行等于上一行错位相加,不足位补 0
[1, 2, 1, 0]
+ [0, 1, 2, 1]
---------------------
= [1, 3, 3, 1]
[1, 3, 3, 1, 0]
+ [0, 1, 3, 3, 1]
---------------------
= [1, 4, 6, 4, 1]
当时我也在纸上比划了半天,为啥我就没观察出来呢?
思路有了,代码就简单了
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
if not numRows:
return []
res = [[1],]
for i in range(1, numRows):
newRows = [a + b for a, b in zip([0] + res[i-1], res[i-1] + [0])]
res.append(newRows)
return res
这个方法一次可以产生一行,复杂度我也分析不出来,感觉好像快了一些,很巧妙啊。
461.汉明距离
两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。
给出两个整数 x 和 y,计算它们之间的汉明距离。
示例:
输入: x = 1, y = 4
输出: 2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
解题思路-461
这个题目主要考察异或。
异或:相同时为0,不同时为1。
示例中 1 和 4 进行异或操作后,第三位和最后一位不同,结果是(0101),只要求出结果中1的个数,就是汉明距离。其中1的个数有两种求法。
第一种
计数二进制字符串中1的个数。
class Solution:
def hammingDistance(self, x: int, y: int) -> int:
return bin(x^y).count('1')
第二种
使用 & 操作,逐次与1相与,如果最末一位是1,相与后结果为1,计数器加1,然后向右移一位继续。
class Solution:
def hammingDistance(self, x: int, y: int) -> int:
count = 0
temp = x ^ y
while temp > 0:
if temp & 1 == 1:
count += 1
temp >>= 1
return count
第三种
还是使用 & 操作,但不是 & 1 ,而是 &(n-1),这个方法每次可以去掉一个 1 位,有几个 1 ,只需要 & 几次。具体的原理,我也说不清楚,大佬的代码,看不懂很正常。
class Solution:
def hammingDistance(self, x: int, y: int) -> int:
count = 0
temp = x ^ y
while temp > 0:
temp &= temp - 1
count += 1
return count
总结
至此,LeetCode 探索模块 初级算法的45道题都结束了。
接下来计划按类型来做题,每个类型的题目集中来搞,学明白后再换一种类型。
以我目前的水准,一道题思考30分钟没有思路,再正常不过了, 即使做出来,离最优解也有很远的距离。 所以做不做出来都无所谓,只要有思考这个过程就行了, 所以现阶段的主要内容就是看题解, 看看最优解是什么样,然后争取把它弄懂。